2025年最新データ対応!ナンバーズ予想プログラムをC++で開発
2025年の最新データを基にした「ナンバーズ」予想プログラムをC++で開発しました。このプログラムは過去の当選データを分析し、次回の当選番号を予測するためのシステムです。予測精度の向上を目指し、フーリエ変換(FFT)など高度なアルゴリズムを駆使して、宝くじ「ナンバーズ3」の当選番号を効果的に予測します。
技術環境と使用プログラム
- メインプログラミング言語: C++ (MFC)
- 開発目的: ナンバーズ3の当選予測精度向上
- 主な技術: フーリエ変換(FFT)、LPF/BPFフィルタ
データ収集と予測手法
本プログラムは「ナンバーズ3」の過去の当選データを収集し、FFT解析を用いて次回の当選番号を予測します。データは公式サイトからCSV形式でダウンロードし、システム内で解析します。
- データ収集: 過去のナンバーズ当選データをウェブからCSV形式で取得
- 予測手法: FFT(フーリエ変換)を使用して、当選番号の周期的傾向を解析
フーリエ変換を用いることで、過去の当選番号がどの程度の周期で出現しているかを特定し、次回の当選確率を高めます。時系列データを周波数ごとに分解し、各周波数の傾向を調べることで、次に来る可能性の高い番号を見つけ出します。
FFT解析と予測アルゴリズムの特徴
このプログラムでは、時系列データに基づいて周波数解析を行い、次回の当選番号を高精度で予測します。特に、以下の手法を活用しています:
- フーリエ変換(FFT): 時系列データを正弦波と余弦波に分解し、各成分の周期性を解析
- LPF(ローパスフィルタ)設定: 高周波ノイズを除去し、より信頼性のある予測を提供
- BPF(バンドパスフィルタ)設定: 特定の周波数帯に注目して、重要な信号を抽出
これにより、過去のデータに含まれるノイズを削減し、正確な当選番号の予測が可能になります。また、C++(MFC)でプログラムを再作成することにより、C#での実装よりも高速化に成功し、より軽量で使いやすいシステムになっています。
フィルタ設定による予測精度の向上
予測精度を向上させるため、プログラムでは以下のフィルタを使用しています:
- LPF(ローパスフィルタ): 不要な高周波成分を除去し、信号のスムージングを行います。これにより、予測の際にノイズが除去され、精度が向上します。
- BPF(バンドパスフィルタ): 特定の周波数成分に注目し、その周波数帯域のみを抽出します。これにより、当選番号に関連する重要な情報を逃さず捉えることが可能です。
これらのフィルタを適用することで、過去のデータに潜むパターンをより明確にし、次に出現する可能性の高い番号を特定します。
使い方と特徴
- データの読み込み: 公式サイトからCSVファイルをダウンロードし、プログラムに読み込みます。
- 解析処理: ダウンロードしたデータを3桁に分解し、各数字に対してFFTを適用します。
- 予測結果の表示: 予測ボタンを押すと、パワースペクトルに基づいて次回の当選確率の高い番号を表示します。最も可能性が高い数字から順にリストアップされます。
数字選択と周期解析による予測の強化
FFT解析を使用することで、各当選番号がどの程度の頻度で出現しているかを解析し、その結果に基づいて次回の当選番号を予測します。周期的に現れるパターンを見つけることで、次に出現する可能性のある番号を確率的に特定します。
このアルゴリズムは、直流成分や基本波、さらには高調波の周期や位相を数式で表すことが可能であり、次回の波形を予測するための指標として活用しています。
無料トライアルで試せる!
本プログラムは6回まで無料で予測を試すことができます。まずは無料で予測機能を体験していただき、その効果を確認してください。その後、ご購入を検討いただけます。
↓ダウンロードは下記からお願い致します。
詳細はお気軽にお問い合わせください。
詳細はお問い合わせください
技術環境と使用プログラム
メインプログラミング言語:VC++
予測手法
データ収集: 過去のナンバーズの当選データをウェブから収集します。
予測: 下記のFFTを使って、次回の当選番号を予測します。
周波数分析とは、ある時系列データについて、①様々な周期を持つ波の加重和として示し、②分析対象
としたい周期の波だけを抽出してその特性を分析する手法のことを指す。
時系列データの中から、ある周波数の波を取り出す手法として、フーリエ変換を用いる。フーリエ変換は、ある時系列データを正弦関数(sinθ)と余弦関数(cosθ)の加重和を用いた数学的表現に
基づいて解析を行う手法であり、電気回路などを扱う電気工学などでは一般的に用いられている。
私は、この解析方法を 「数字選択式宝くじ ナンバーズ3」 に応用しました。
「ナンバーズ」の各桁ごとの当選番号を 調べると、ある当選番号は周期的に出ている傾向があります。
この傾向を調べることにより 「どの当選番号がどの程度の割合」 で発生しているか?
ということを解析でき、次回の「当選番号」予測に応用するものです。
10年間、過去の膨大なデータをもとにすべての研究成果を注ぎ込んで、当選確率を上げるFFT解析アルゴリズムを徹底的に研究してきました。
C++(MFC)で再作成し完成しました。C#より高速化に成功。軽量でかつ使いやすいです。
ナンバーズ3は、セットの購入がおすすめです。
5の予想
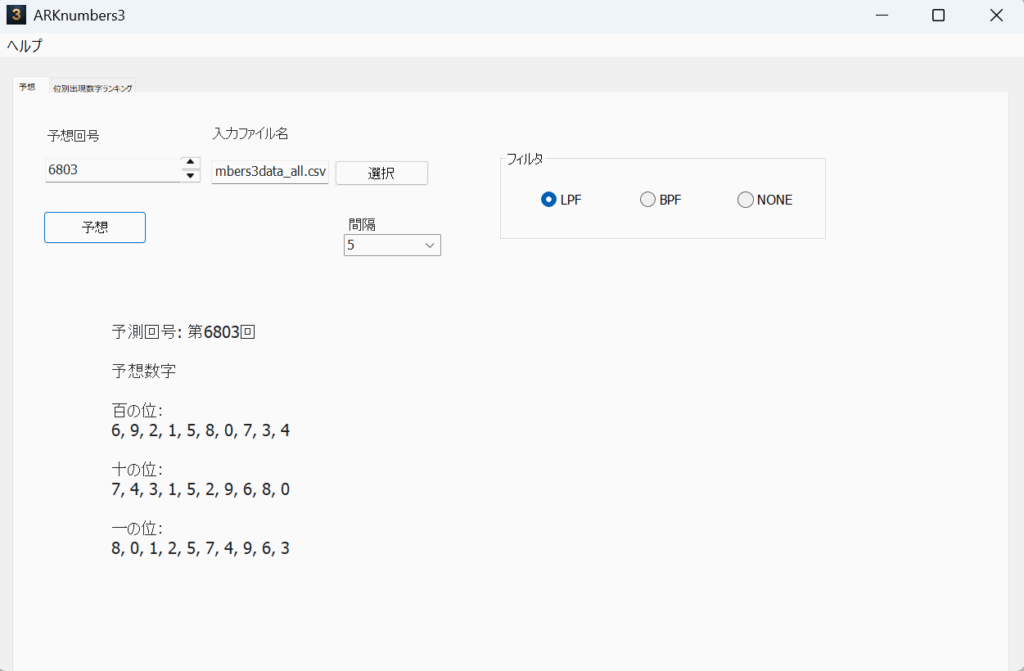
10の予想
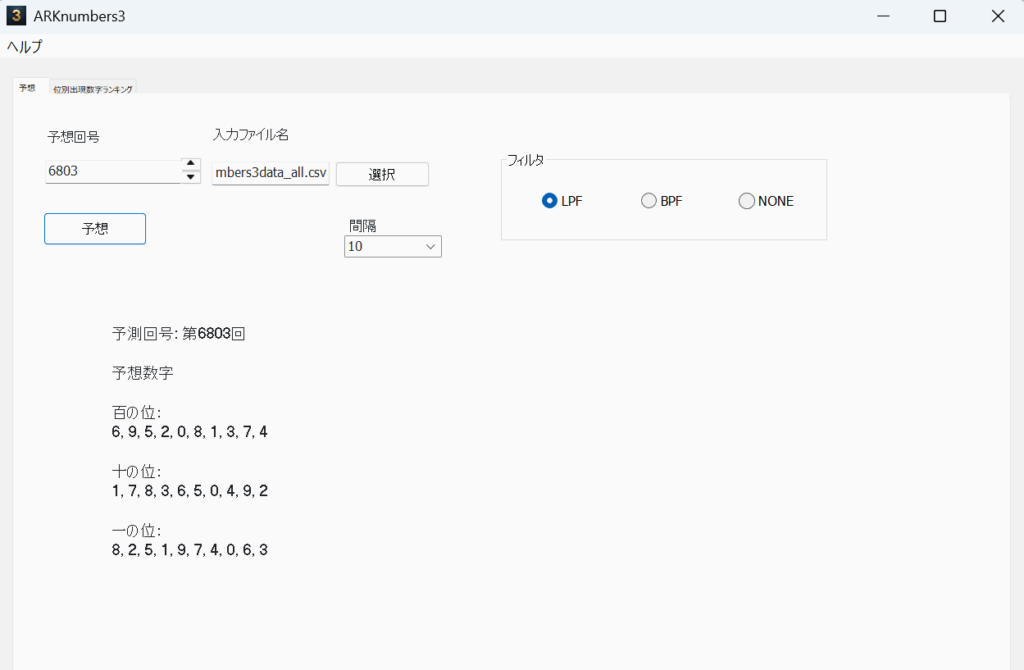
15の予想
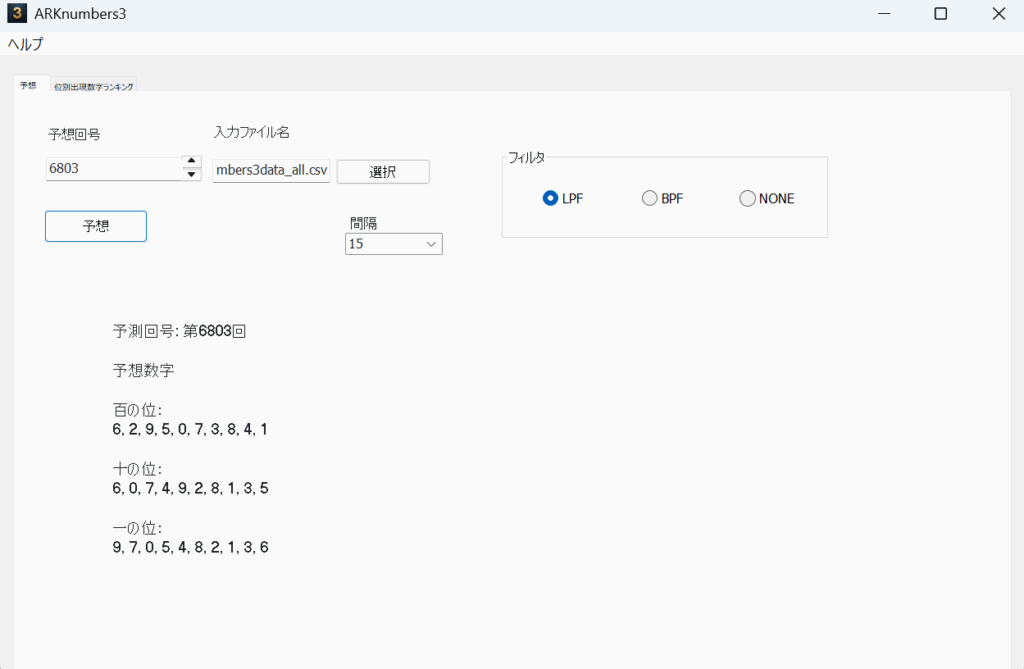
20の予想
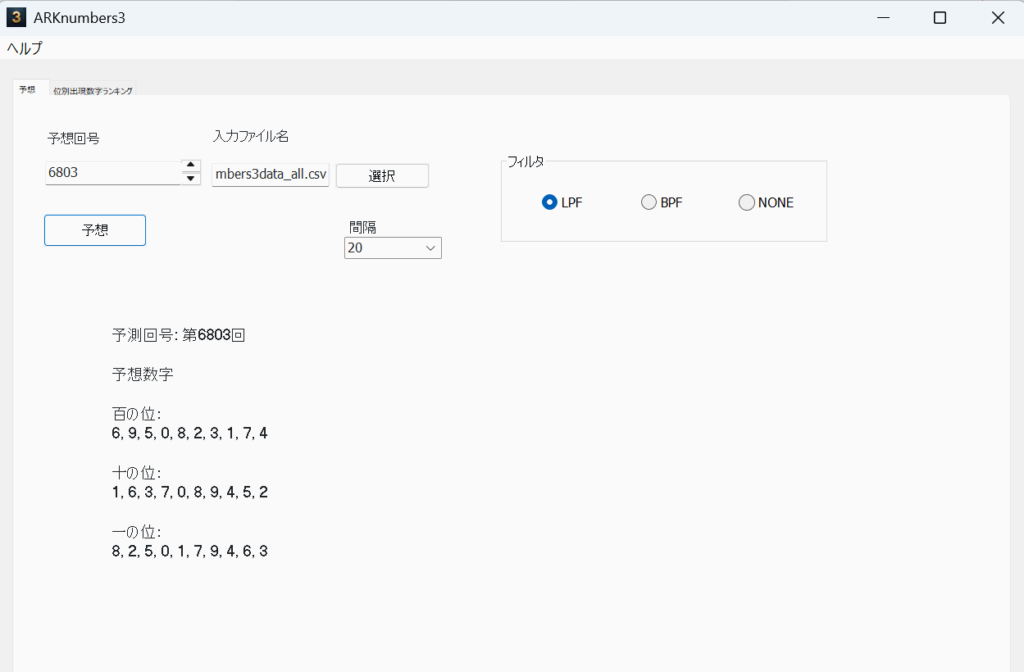
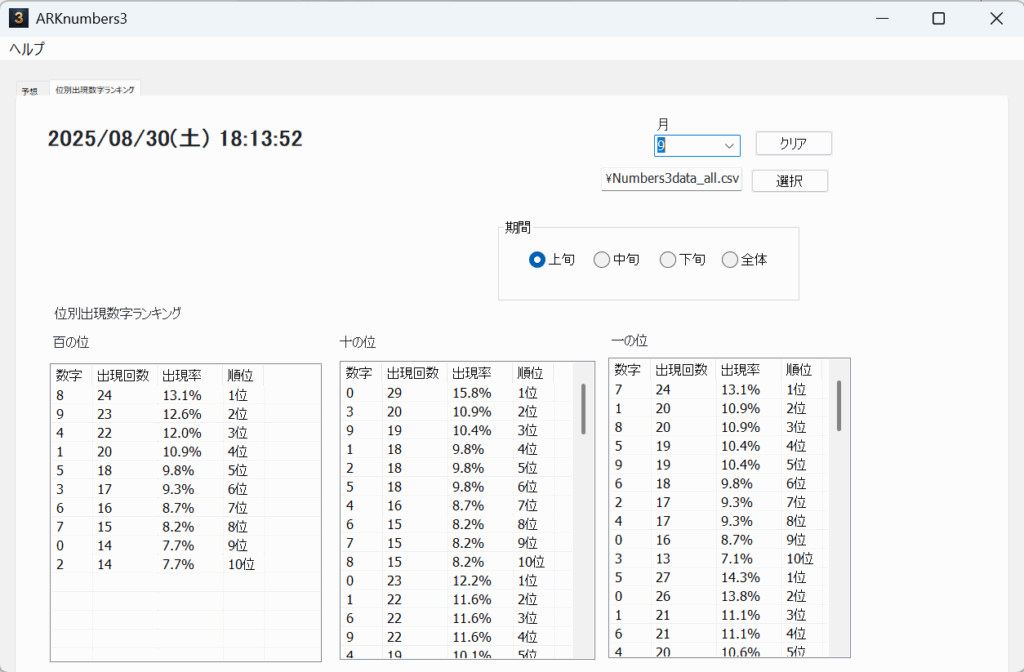
横の数字(1-15)は、それぞれの当選番号が何回目に出現したか?という周期。
縦の数字(0-9)は、各桁毎の当選番号とその出現回数。
上記を配列に格納して、それぞれの数字にFFTを行う。
当せん番号の分析(ナンバーズ3) – 宝くじ(ロト・ナンバーズ) – PayPay銀行 (paypay-bank.co.jp)
上記サイトからCSVファイルでダウンロードします。
予想したい回号を入力して、さきほどダウンロードしたCSVファイルを選択します。
CSVファイルを読み込み、3桁に分解し、可変長配列に格納します。
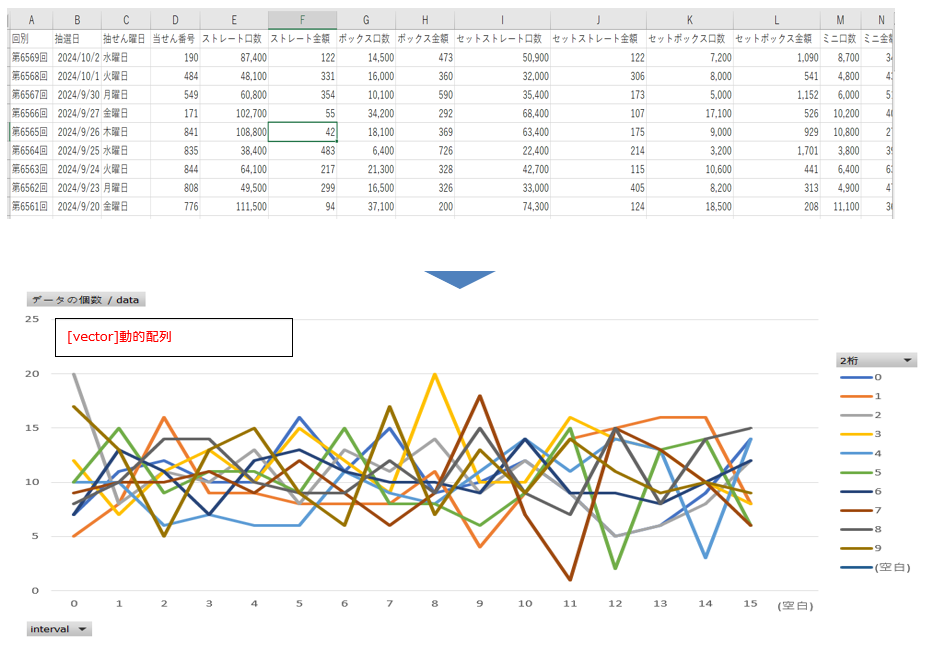
予測ボタンを押すと簡易ラベルに予想のパワースペクトルが表示されます。
強さに基づいて予測結果をソートし、最も強い(=最も次に来る可能性が高い)数字を順に表示します。
ある周期関数を構成している直流成分や基本波、第二次高調波、第三次高調波の振幅や周期、位相を数式で表すことができる。周期関数を構成している各成分の数式がわかるということは、次に発生する
波形の値を計算で求め予測することができるということになります。
高速フーリエ変換(FFT)をC++で実装する方法について説明します。ここでは、最も一般的なラディックス-2のコーリー・トゥーキーアルゴリズムを使用する。このアルゴリズムは、データサイズが2のべき乗である場合に特に効率的である。
下記コードの一例です。次回からこのソフトを使用して予想を発表していきます!
C++によるFFTの実装(例)
まず、必要なライブラリをインクルードし、複素数を扱うために<complex>を使用する。
#include <iostream>
#include <vector>
#include <complex>
#include <cmath>
const double PI = 3.141592653589793238460;
次に、FFTの主要な関数を定義します。
ビット逆順ソート
FFTの効率を高めるために、入力データをビット逆順に並べ替える必要がある。
void bitReverse(std::vector<std::complex<double>>& data) {
int n = data.size();
int j = 0;
for (int i = 0; i < n; ++i) {
if (i < j) {
std::swap(data[i], data[j]);
}
int m = n >> 1;
while (m >= 1 && j >= m) {
j -= m;
m >>= 1;
}
j += m;
}
}
FFTアルゴリズム
次に、ラディックス-2のFFTアルゴリズムを実装する。
void fft(std::vector<std::complex<double>>& data) {
int n = data.size();
bitReverse(data);
for (int s = 1; s <= std::log2(n); ++s) {
int m = 1 << s;
std::complex<double> wm = std::exp(std::complex<double>(0, -2.0 * PI / m));
for (int k = 0; k < n; k += m) {
std::complex<double> w = 1.0;
for (int j = 0; j < m / 2; ++j) {
std::complex<double> t = w * data[k + j + m / 2];
std::complex<double> u = data[k + j];
data[k + j] = u + t;
data[k + j + m / 2] = u - t;
w *= wm;
}
}
}
}



コメント